Algorithms are commonly taught in Computer Science, Software Engineering subjects at your Bachelors or Masters. Some find it difficult to understand due to memorizing them without practically going through those algorithms. There are many sorting algorithms present today. I’ll be going through some of the commonly taught algorithms in Computer Science / Software Engineering.
Bubble Sort
It’s a simple algorithm starting from the L.H.S (Left-hand Side) and repeatedly compares the adjacent values and keep swapping (bubbling) the larger ones to the R.H.S(Right Hand Side). Which can be represented in the following repetitions.
First Cycle
| First Step | [ 4 0 3 1 7 ] –> [ 0 4 3 1 7 ], In here Bubble sort compares the first two values and swaps 5 with 1.(The largest one to the left). |
| Second Step | It continues the cycle with the second value by comparing the third [ 0 4 3 1 7 ] –> [ 0 3 4 1 7 ], and Swap since 4 is greater than 3. |
| Third Step | Again it compares the third with fourth elements [ 0 3 4 1 7 ] –> [ 0 3 1 4 7 ], Swap 4 with 1, since 4 is greater than 1. |
| Fourth Step | It compares the fourth with fifth [ 0 3 1 4 7 ] –> [ 0 3 1 4 7 ] and the value 4 is less than 7, therefore the value will not get swapped. |
Second Cycle
It continues the steps to the same steps to swap the values as shown in cycle one.
| First Step | [ 0 3 1 4 7 ] –> [ 0 3 1 4 7 ] |
| Second Step | [ 0 3 1 4 7 ] –> [ 0 1 3 4 7 ], It will Swap 3 with 1 due to 3 is greater than 1. |
| Third Step | [ 0 1 3 4 7 ] –> [ 0 1 3 4 7 ] |
| Fourth Step | [ 0 1 3 4 7 ] –> [ 0 1 3 4 7 ] |
Third Cycle
In the third cycle, it checks whether there is a necessity to swap any elements. If there is no swapping needed the algorithm will stop in this phase.
| First Step | [ 0 1 3 47 ] –> [ 0 1 3 47 ] |
| Second Step | [ 0 1 3 4 7 ] –> [ 0 1 3 4 7 ] |
| Third Step | [ 0 1 3 4 7 ] –> [ 0 1 3 4 7 ] |
| Fourth Step | [ 0 1 3 4 7 ] –> [ 0 1 3 4 7 ] |
It can be represented in a Python programming language as below.
# Python program to implement bubbleSort
# BH
# Array input to swap
arr = [4 , 0 , 3 , 1 , 7]
def bubbleSort(arr):
n = len(arr)
# Going through all array elements
for x in range(n):
# Last x elements are already in place
for y in range(0, n-x-1):
# going through the array from 0 to n-x-1
# Swap if the element found is greater than the next element
if arr[y] > arr[y+1] : arr[y], arr[y+1] = arr[y+1], arr[y]
bubbleSort(arr)
print ("Sorted elements are :")
for x in range(len(arr)): print ("%d" %arr[x]),Output:
Sorted elements are :
0
1
3
4
7
Selection Sort
It’ll go through all the elements and find the smallest one then It’ll Swap the element into that position as the first item. It’ll continue to repeat the selection sort on the remaining items (N – 1).
Finding the smallest value from the Array and place it at the beginning
| First Step | [ 2 4 1 7 9 ] -> [ 1 4 2 9 7 3 ] |
| Second Step | [ 1 [ 4 2 7 9 ] ] -> [ 1 2 4 7 9 ] |
| Third Step | [ 1 2 [ 4 7 9 ] ] -> [ 1 2 4 7 9 ] |
| Fourth Step | [ 1 2 4 [ 7 9 ] ] -> [ 1 2 4 7 9 ] |
# Implementing Selection Sort in Python
# BH
import sys
Sort_Array = [ 2, 4, 1, 7, 9]
# Going through all array elements
for x in range(len(Sort_Array)):
# Find the minimum element in remaining unsorted array
min_idx = x
for z in range(x+1, len(Sort_Array)):
if Sort_Array[min_idx] > Sort_Array[z]:
min_idx = z
# Swap minimum element with the first element
Sort_Array[x], Sort_Array[min_idx] = Sort_Array[min_idx], Sort_Array[x]
# Driver code to test above
print ("Sorted array : ")
for x in range(len(Sort_Array)):
print("%d" %Sort_Array[x]),
Output :
Sorted array :
1
2
4
7
9Insertion Sort
Insertion sort is based on the concept where in each iteration one element is taken to find it’s relevant position to where it beleongs in a sorted array.

It is less efficient in terms of larger array elements comparing to other sorting algorithms like heapsort, mergesort or quicksort.
By each iteration, it grows the sorted array and it compares the element with the largest element in the sorted array. If the current element is greater in value then it leaves the current element and moves to the next iteration and then it checks the element, If it’s less than the sorted array then it moves to the relevant position. This is done by shifting the larger elements than the current element in the sorted array. This process is repeated until all elements are sorted.
# Implementing Insertion Sort in Python
# BH
number_array = [5,7,3,10,2,8]
def insertionSort(number_array):
# Going through 1 to length of array
for x in range(1, len(number_array)):
key = number_array[x]
# Move elements of Array that are greater than key to one position ahead of their current position
no = x-1
while no >= 0 and key < number_array[no] :
number_array[no + 1] = number_array[no]
no -= 1
number_array[no + 1] = key
# Printing the sorted array
print ("Sorted array : ")
insertionSort(number_array)
for y in range(len(number_array)):
print ("% d" % number_array[y])
Output :
Sorted array :
2
3
5
7
8
10Quick Sort
Quicksort picks an element as Pivot and divides the given values (array) around the picked pivot. Quick Sort is similar to Merge Sort and it’s a Divide and Conquer algorithm.
QuickSort helps to lessen the space complexity and removes the use of additional array which is used in Merge Sort. In Most cases selecting a pivot in an array improve the time complexity. There are many ways to pick a Pivot element.
How to Implement Quick sort?
These are the steps to implement a quicksort algorithm.
- Step 1: I have selected the pivot as the last index of the array after selecting the pivot, We have to divide the array using Partitioning.
- Step 2: Quick Sort uses Partitioning to divide the array into two subarrays, but when it comes to partitioning, the elements which are smaller than the pivot will be on the left-hand side of the pivot and the elements which are greater than the pivot will be on the right-hand side of it And the pivot element will be at its final sorted position.
- Step 3: The array elements which are at the left-hand side and right-hand side may not be sorted.
- Step 4: Then the sub-arrays with the elements on the left-hand side of pivot and elements on the right-hand side of pivot will be portioned by choosing a pivot in the subarrays.

It can be represented in a Python program as below.
# Implementing Quick Sort in Python
# BH
quicksort_array = [40,33,3,11,50,48]
def partition(quicksort_array,starting_index,ending_index):
i = ( starting_index-1 ) # index of smaller element
pivot = quicksort_array[ending_index] # pivot
for j in range(starting_index , ending_index):
# If current element is smaller than the pivot
if quicksort_array[j] < pivot:
# incrementing the smaller element
i = i+1
quicksort_array[i],quicksort_array[j] = quicksort_array[j],quicksort_array[i]
quicksort_array[i+1],quicksort_array[ending_index] = quicksort_array[ending_index],quicksort_array[i+1]
return ( i+1 )
# Quick sort Function
def quickSort(quicksort_array,starting_index,ending_index):
if starting_index < ending_index:
# partitioning index variable is pi
pi = partition(quicksort_array,starting_index,ending_index)
# Separately sort elements before partition and after partition
quickSort(quicksort_array, starting_index, pi-1)
quickSort(quicksort_array, pi+1, ending_index)
quickSort(quicksort_array,0,len(quicksort_array) -1)
# Printing the sorted array
print ("Sorted array :")
for i in range(len(quicksort_array) ):
print ("%d" %quicksort_array[i])
Output :
Sorted array :
3
11
33
40
48
50Merge Sort
Merge Sort is like Quick Sort where It uses Divide and Conquer algorithm strategy. It breaks the input array into two halves and then runs the algorithm for the two halves then merges the sorted two halves.
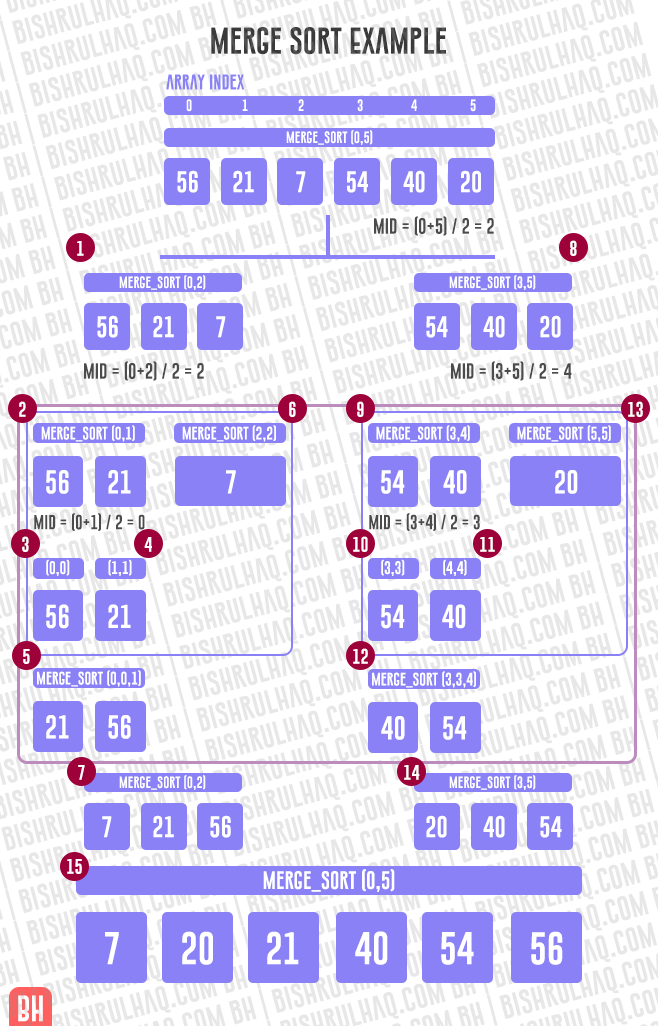
While comparing two halves for merging, the first element of both lists is taken into consideration. While sorting in the correct order, The lower value element becomes a new element of the sorted list. This method is repeated until both the smaller halves are empty and the new combined subarrays comprise all the elements of both the subarrays.
# Python program to implement MergeSort
# BH
mergeArray = [56,21,7,54,40,20]
def mergeSort(mergeArray):
if len(mergeArray) > 1:
mid = len(mergeArray) // 2
before_left = mergeArray[:mid]
before_right = mergeArray[mid:]
# Recursive call on each half
mergeSort(before_left)
mergeSort(before_right)
# Two iterators for going through the two halves
i = 0
j = 0
# Iterator for the main list
k = 0
while i < len(before_left) and j < len(before_right):
if before_left[i] < before_right[j]:
# The value from the half has been used
mergeArray[k] = before_left[i]
# Move the iterator forward
i += 1
else:
mergeArray[k] = before_right[j]
j += 1
# Move to the next slot
k += 1
# For all the remaining values
while i < len(before_left):
mergeArray[k] = before_left[i]
i += 1
k += 1
while j < len(before_right):
mergeArray[k]=before_right[j]
j += 1
k += 1
print ("Array Before Sorting : ", *mergeArray)
mergeSort(mergeArray)
print ("Array After Sorting : ", *mergeArray)Output :
Array Before Sorting : 56 21 7 54 40 20
Array After Sorting : 7 20 21 40 54 56